Atmosphere! study about basic of the atmosphere is important in aerodynamics as it will tell us about what is pressure, density, temperature, specific volume flow velocity and streamline with its most commonly used units in aerodynamics it will also brief us about which are the 6 different types of altitude, hydrostatic equation
PRESSURE
The pressure is a normal force
per unit, area exerted on the surface due to the time rate of change of momentum
of the gas molecules on that surface. It is usually defined at a point in the
gas or a point on a surface and can vary from one to another.
Commonly
used units of pressure are
- Newton per square meter (N/m2)
- Dynes per square centimetre (Dyn/cm2)
- Pounds per square foot (lb/ft2)
- Atmospheres (atm)
DENSITY
The density of a substance including gas is the mass of that substance per unit volume.
Density will be designated by symbol r
Commonly
used units of density are
- kilogram per cube meter (kg/m3)
- slug per cube foot (slug/ft3)
- pound per cube foot (lbm/ft3) (1 slug=32.2Ibm)
TEMPERATURE
Temperature is the measure of the average kinetic energy of the particles in the gas.
Commonly
used units of temperature are
- kelvin (K)
- degree Celsius (°C)
- degree Rankine (°R)
- degree Fahrenheit (°F)
SPECIFIC VOLUME
r is mass per unit volume. Inverse
if r
is called a specific
volume i.e. volume per unit mass
Units
- m3/kg
- ft3/slug
FLOW VELOCITY
Velocity is the distance travelled by an
object with respect to time, we all know what 40 m/s velocity of a vehicle
means. When we talk about flow velocity it is more subtle as 40 m/s due to
south in a horizontal plane. It is very important to designate both speed and
direction of flow velocity.
Each
region of gas doesn't need to have the same velocity, it will vary point to
point. Flow velocity varies, along with p (pressure), r(density), T (temperature) is a point property
The velocity
at any fixed point in the flowing gas is the velocity of an infinitesimally a small fluid element as it sweeps through point.
STREAMLINES
The path took by a
moving fluid element is called as streamlines of the flow. There can be no flow across
streamlines
DIFFERENT TYPES OF ALTITUDE
There
are 6 types of altitude
- Pressure altitude
- Temperature altitude
- Density altitude
- Absolute altitude
- Geometric altitude
- Geopotential altitude
Absolute altitude (ha): The distance measured from the centre of the earth
Geometric altitude: it is defined as the distance
measured from the ground from the fig, we can say that
From fig 1 we can say that
From newton’s law of gravitation (g varies inversely
as the square of the distance from the centre of the earth)
g=
local acceleration of gravity
g0= gravitational
acceleration at sea level
r= radius of the earth
hG=geometric altitude
ha= absolute altitude
We will take
a model which will allow us to calculate the variation of r,p,
T as the function of altitude
Consider the small stationary fluid element in air
as shown in fig 2.
We take rectangular faces where dhG is
the height of the side face of the rectangle which is infinitesimally small.
We will take a model which will allow us to calculate the variation of r,p, T as the function of altitude
We will take a model which will allow us to calculate the variation of r,p, T as the function of altitude
Consider
the small stationary fluid element in the air as shown in the fig.
We take
rectangular faces where dhG is the height of the side face of the rectangle which is infinitesimally small.
On the
bottom face, the pressure p is felt which gives rise to upwards force of p×1×1
exerted on the fluid element & the top surface is slightly at higher altitude
by the distance of dhG,
The pressure differs from the infinitesimal
value of dp hence, the pressure felt by the top surface is p+dp. It gives rise
to a downwards force of (p+dp)(1)(1)on the fluid element.
The volume of the fluid element is (1)(1)dhG
= dhG.
Mass of
the fluid element is rdhG. The weight of the
fluid element is grdhG.
Pressure
forces and weight must be balanced because the element is in the rest position
Equation
number 2 is in a differential form we will integrate this equation to get the
variation of pressure in terms of altitude assuming g is constant throughout
the atmosphere which is equal to g0
Altitude
h in equation 3 must be different from hG in equation 2 to
compensate for the fact that g is slightly different from g0. We
have defined a new altitude h, which is geopotential altitude. In practical
geopotential altitude is a "fictitious" altitude
RELATION
BETWEEN GEOPOTENTIAL AND GEOMETRIC ALTITUDES
By convention, we will set
both h and hG equal to zero at sea level. Now, consider a given
point in the atmosphere. This point is at a certain geometric altitude hG
, and associated with it is a certain value of h (different from hG,)
integrating equation 5 between the sea level and given point we get

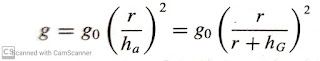





No comments:
Post a Comment